 ㈱ジャパンデンタル
㈱ジャパンデンタル
執行役員企画本部長兼システム部長
入江 英之
1.統計データを見るうえでの注意点
現代社会において、統計データは意思決定や問題解決に欠かせない重要な情報源です。本稿では、統計データを正確に理解し活用するために、基本的な注意点について解説します。
まず、平均値だけに頼らないことが重要です。平均値は一般的に使用されることが多く、通常はこれで十分ですが、重要な意思決定を行う場合など、統計データが重要な判断根拠となる場合は、平均値以外にも確認すべき指標(代表値)があります。平均値はデータの中心傾向を示す一方で、データのばらつきや外れ値(異常値)の影響を受けやすく、データ全体の把握には不十分な場合があります。例えば、極端に大きな値や小さな値が存在する場合、それらが平均値に大きな影響を与え、実際のデータの分布を誤解させることがあります。
そのため、統計データを正確かつ総合的に理解するためには、中央値や最頻値などの他の指標(代表値)も併用することが必要です
次に、データのばらつきや分散を見ることが重要です。分散や標準偏差は、データが平均値からどれだけ離れているかを示す指標です。これらの指標を用いることで、データの広がりやばらつきを定量的に把握することができます。分散が大きい場合、データは平均値から大きく離れていることを意味し、分散が小さい場合、データは平均値の近くに集中していることを意味します。平均値が同じであったとしても、分散が大きい場合は数値の上下差が大きく、平均値から見た上下差も大きく離れていることになります。
2.指標(代表値)について
(1)平均値
平均値(mean)は、全データの総和をデータの個数で割った値です。すべてのデータが計算に含まれるため、極端な値の外れ値などの影響を受けやすくなります。一般的にデータの中心的傾向を示すのに使用されますが、後記のグラフ①②の通り、正規分布(左右対称の釣鐘型グラフ)でない場合や外れ値(異常値)が存在する場合は、平均値が全体の傾向を正確に反映しないことがあります。
(2)中央値
中央値(median)は、データを小さい順または大きい順に並べたとき、真ん中に位置する値です。データの分布の形に影響を受けず、外れ値(異常値)の影響を受けにくいため、特にデータが偏っている場合や外れ値(異常値)が多い場合に有効です。
(3)最頻値
最頻値(mode)は、データ内で最も頻繁に出現する値です。一番多く出現する値であり、データの分布の形に影響を受けず、外れ値(異常値)の影響を受けにくいため、カテゴリーデータや特定の値の頻度を知りたい場合に有効です。
(4)分散
分散(variance)は、データの各値が平均値からどれだけ離れているかを示す指標です。分散が大きいほど、データのばらつきが大きいことを意味します。
(5)標準偏差
標準偏差(standard deviation)は、分散の平方根で、データのばらつきを直感的に理解しやすい形で示します。標準偏差が小さいほど、データは平均値の周りに集まっていることを意味します。
3.グラフの活用
後記のグラフ①②を見ていただければ、平均値だけに頼り過ぎると誤解したり、間違った判断をする可能性があることが、お分かりいただけるのではないでしょうか。
統計データを正確に理解するためには、複数の指標を併用し、データのばらつきや分布を総合的に把握することが重要です。これにより、データの全体像をより正確かつ総合的に捉え、適切な意思決定や問題解決に役立てることができます。
<グラフ①>
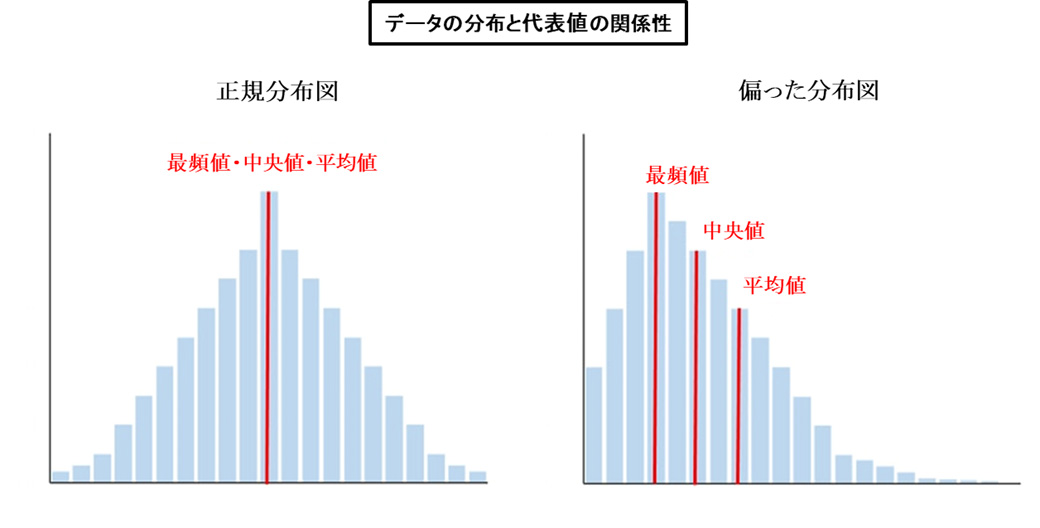
<グラフ②>
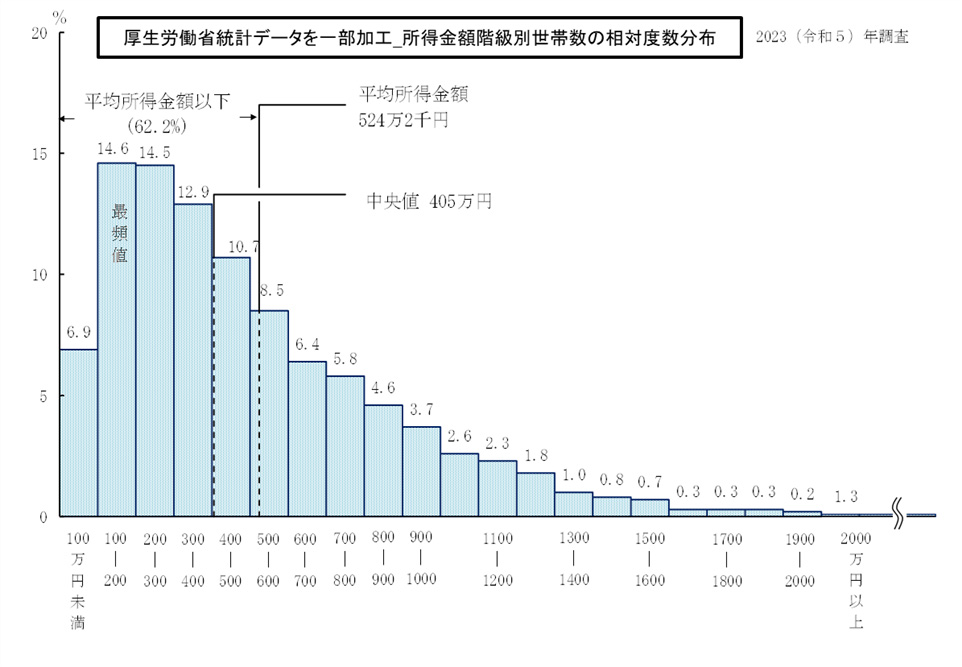
以上

